What is cornering?
If every F1 driver had the exact same car, the winner would be determined by their cornering skills. Cornering is the act of taking a turn in a race. It is a lot more complicated than just staying in the lines. If you follow the middle of the track the entire time, you will lose a lot of speed and may run off the track. Imagine taking a 90 degree turn at 80mph (which is slower than some of the turns F1 cars take): you will probably end up locking up and crashing trying to take such a tight corner at that speed. This is why drivers follow racing lines that allow them to maximize their speed around turns. The faster an F1 car goes, the greater downforce it experiences, leading to faster cornering speeds. Nothing can beat an F1 car around a corner.
There are three main parts of a corner: the turn in (entry), apex, and exit. Drivers position and brake prior to the corner.
To get the maximum speed throughout the corner, the racing line the car must take looks something like this:
If you are interested in the physics behind the racing line, take a look at the diagram and explanation provided at the end of the article.
Additionally, drivers can choose to hit the apex early or late. The racing line will change accordingly:
Drivers may do this depending on where they want to be positioned for the next corner or straight.
G-Forces
G-force is simply the force due to gravity. Formula 1 cars can take a corner as fast as 300kph (186mph) which means that the driver can pull up to 4-6 gs during the cornering process. Drivers experience vertical and lateral gs but the lateral gs are the ones that have the most impact on drivers. These occur when the car is braking, accelerating or taking a corner. G-forces can disrupt blood flow and cause certain parts of your body to stop working. That is why drivers have to be in the best shape to be able to withstand these forces at such a high level.
Diagram and Explanation of the Racing Line
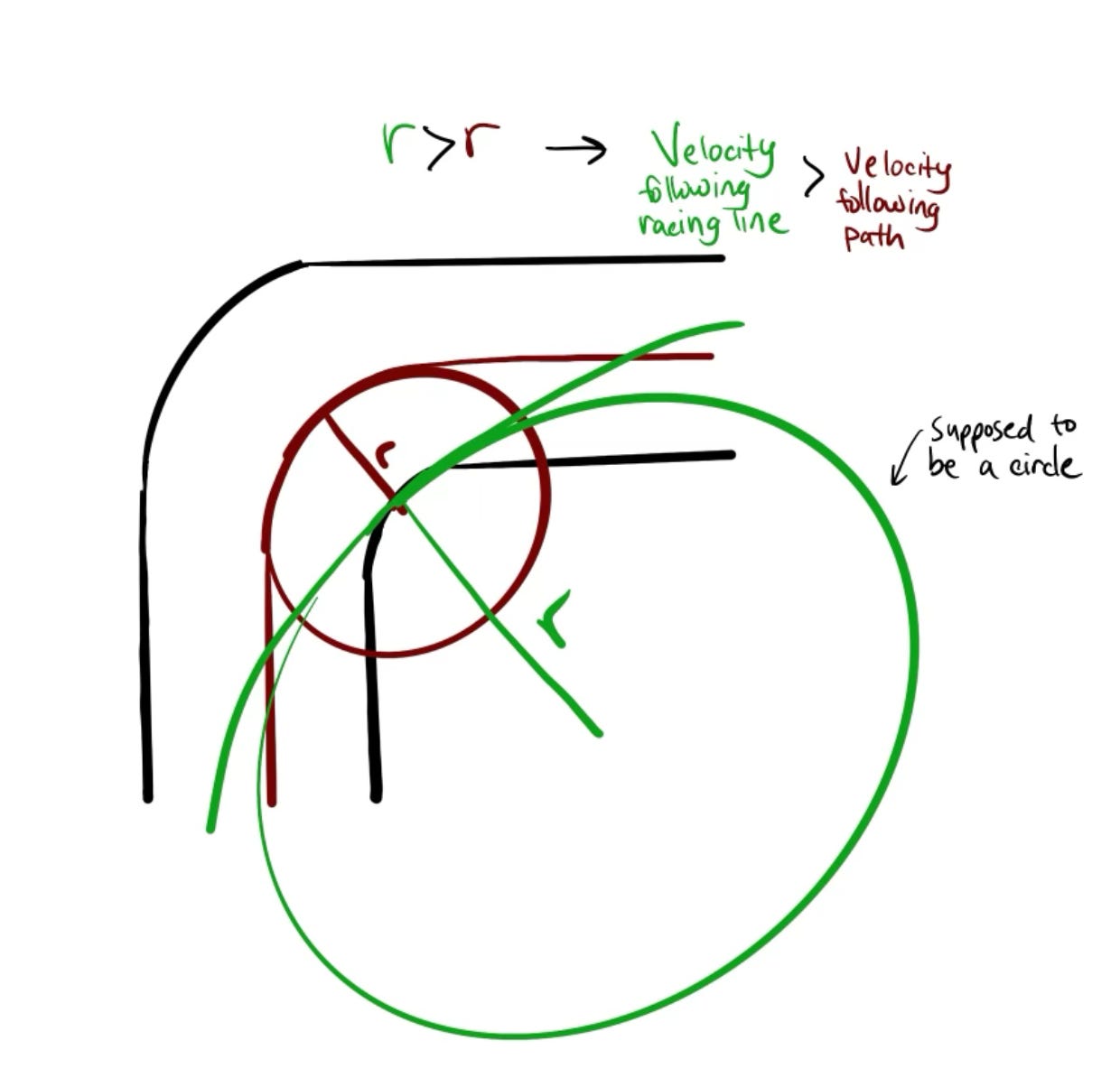
We can explain racing lines by exploring the relationship between radius and velocity.
Using angular velocity to find the relationship between radius and translational velocity:
The greater the radius, the greater the translational velocity is. This is because you know that the velocity is equal to distance over time. In a circle we call distance arc length or S. So the change in arc length over change in time will equal your velocity (ΔS/Δt = v). We also know that arc length is equal to the radius times the angle (S = rθ). If you think about the circumference of a circle, it is known to be 2πr. The angle that the object goes around in a circle is 2π radians (360 degrees). Thus, the arc length can be known as the angle in radians traveled times the radius. Then, you know translational velocity to be Δθr/Δt (change in angle x radius over the change in time). This is also your angular velocity w (change in theta over change in time) x r. So we know v = rw.
Thus, as radius increases your translational velocity increases too. So, to get the maximum speed around a corner, you must maximize radius. This is why the drivers don’t just drive down the center of the track.
Using Centripetal Acceleration to explain racing lines
Additionally, if you take a small radius turn at a high speed, you run the risk of losing friction and spinning out. By Newtons second law of motion we know that F = ma and knowing that the acceleration (which is centripetal acceleration) is equal to v^2/r and the force to be friction we can then manipulate the equation to be friction (which is the centripetal force) x radius = velocity^2. Thus, as radius increases, the velocity increases as well which supports the conclusion from the other method.
Sources
https://d3cm515ijfiu6w.cloudfront.net/wp-content/uploads/2022/05/21164406/lewis-hamilton-spanish-grand-prix-qualifying-planetf1-1200x630.jpg
Kristensen, Stefan. “Formula 1 and G-Forces: All the Fun Facts - Motorsport Explained.” Motorsport Explained -, 16 October 2021, https://motorsportexplained.com/f1-g-forces/. Accessed 1 October 2022.
https://lifeatlean.com/wp-content/uploads/2012/04/images_BasicRacingLine.jpg








There's a saying that what makes F1 cars so fast are the brakes. In addition to following the racing line, F1 drivers are able to dynamically adjust the brake bias (or brake balance) using controls on the steering wheel. This gives them control over the balance of braking force between the front and rear wheels for each turn. So when they go into a sharp turn after a long straight, the driver wants front bias to give them more stopping power, and when they are going into a softer corner, they want more rear bias, allowing them to rotate the car into the turn. What's amazing is that the drivers are managing the brake balance in real time, while overtaking (or being overtaken) and experiencing 4-5g on their body!